The gravity field in Iceland
and the foundations of the land
Research results 1988-1992
In the years around 1990 we, Stefán G. Magnússon and Freyr Þórarinsson, carried out various kinds of research on gravitational field and magnetic fields, working both on developing research methods and on the processing of Icelandic data. The data was obtained from the National Energy Authority and the Science Institute of the University of Iceland and our co-authors of the articles on the data processing were from those institutions.
The first phase of our research focused on developing methods to analyse directionality in maps of gravitational and magnetic fields and topography. To do this, we wrote computer programs that used two-dimensional Fourier transforms to turn a map into a directional power spectrum. We wrote papers about this work, e.g. a paper in Geophysics. Another paper appeared in Jökull a year later, where these methods were applied to data from Southwest Iceland.
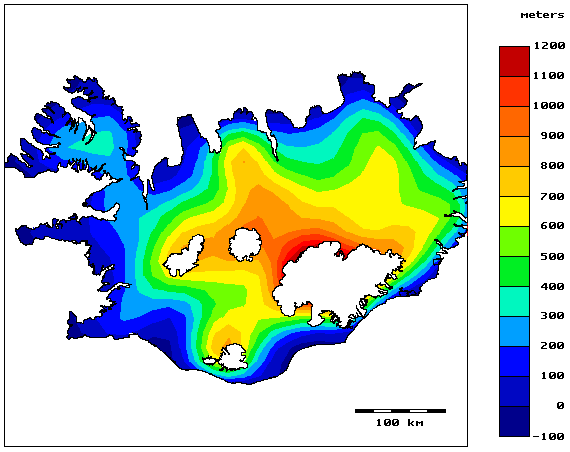
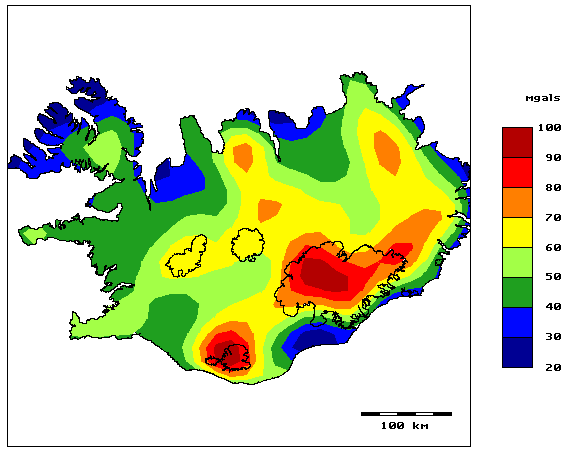
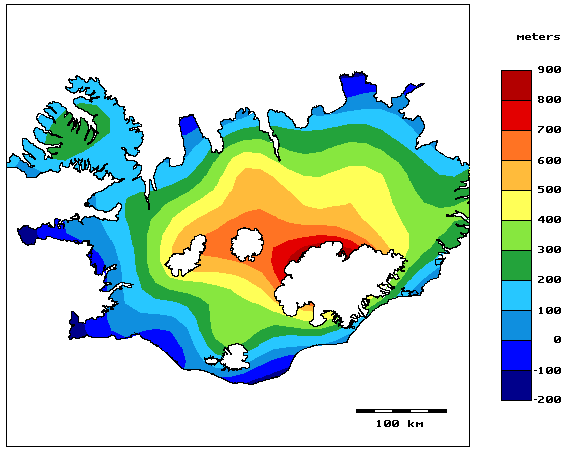
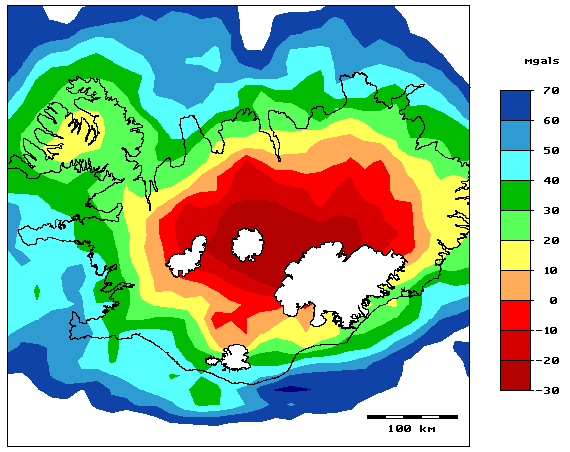
One of the things to consider in processing gravity data is the choice of Bouguer density used correct the effects of landscape in the measurements. A common approach to this is to minimize the correlation between landscape and corrected gravity field (often referred to as Nettleton's method), but we soon realized that this method was not always suitable for Icelandic data. The reason is that this method assumes the landscape to be resting on a rigid inflexible substrate, while in Iceland the crust is thinner and more flexible than on the continents where Nettelton's method was developed. So we developed another method based on minimizing the fractional width of the corrected gravitational field and published it in a paper in Geophysics.
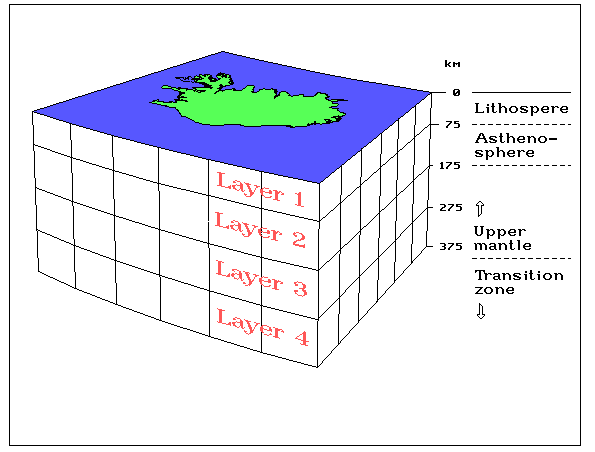
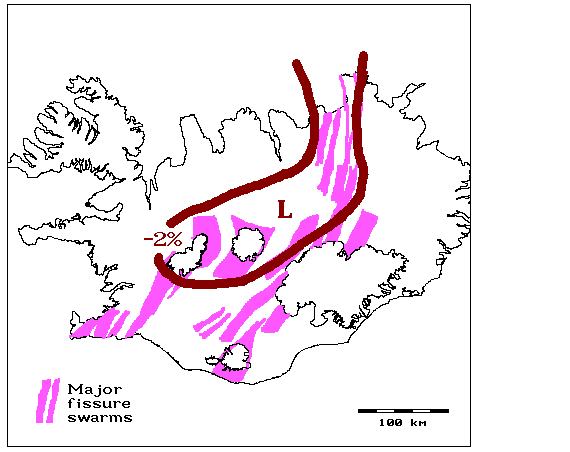
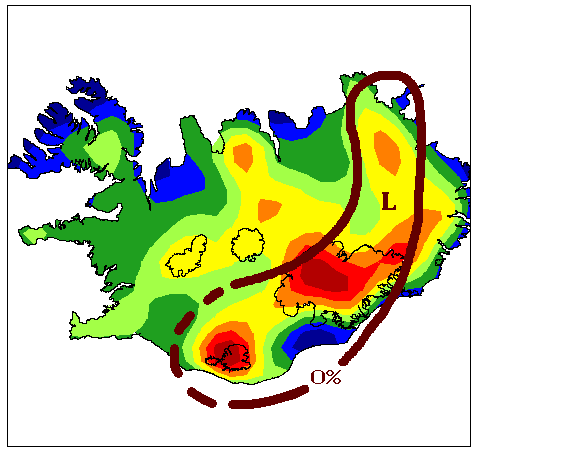
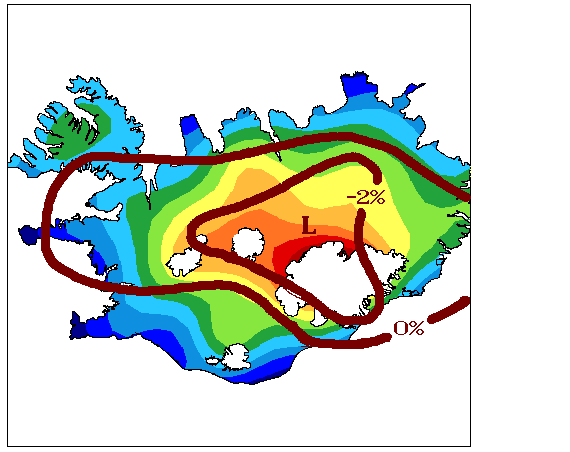
The research on suitable Bouguer density focused our attention on the load-bearing capacity of the Icelandic earth's crust and the boundary between rigid landscapes and floating, and the main findings of our research in this area are discussed alongside figures 1-3 below. Then we got acquainted with the paper by Kristján Tryggvason et al. showing a seismic image of the hot spot beneath Iceland, and found that what was shown there seemed to be in good agreement with our research (figures 5-8). These ideas were presented in various ways at several conferences in Iceland and abroad, but before articles about them were published in magazines, both of us had turned to other subjects. However, the idea has survived to give an account of these discussions in an accessible place, and that is why this website has now been created.
More than three decades have passed since the material presented here was created, but no attempt has been made to update it in light of new results. The reader can therefore imagine this to be a message in a bottle that he receives long after its contents were created. Comments on the topic can be sent to freyrth@hotmail.com.